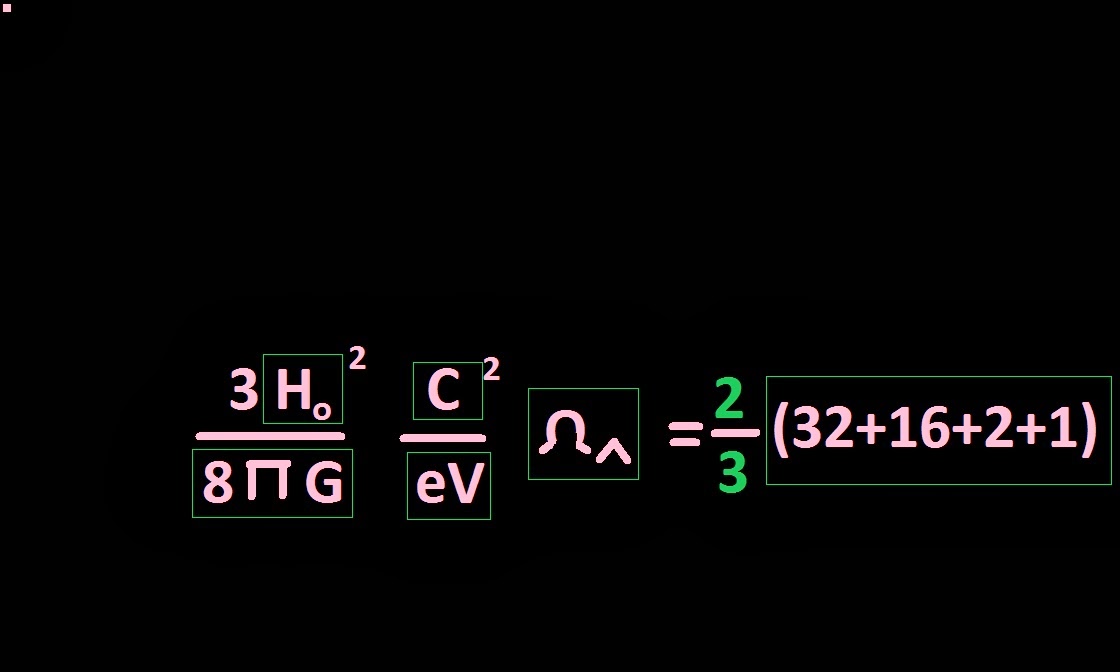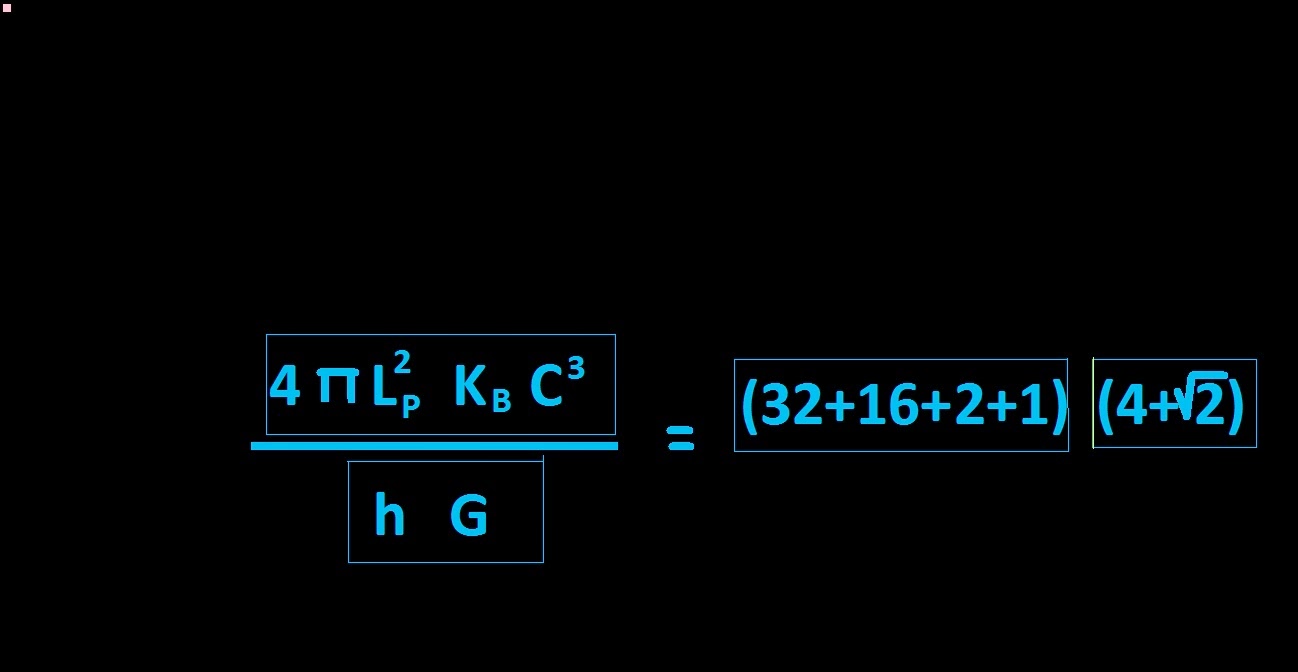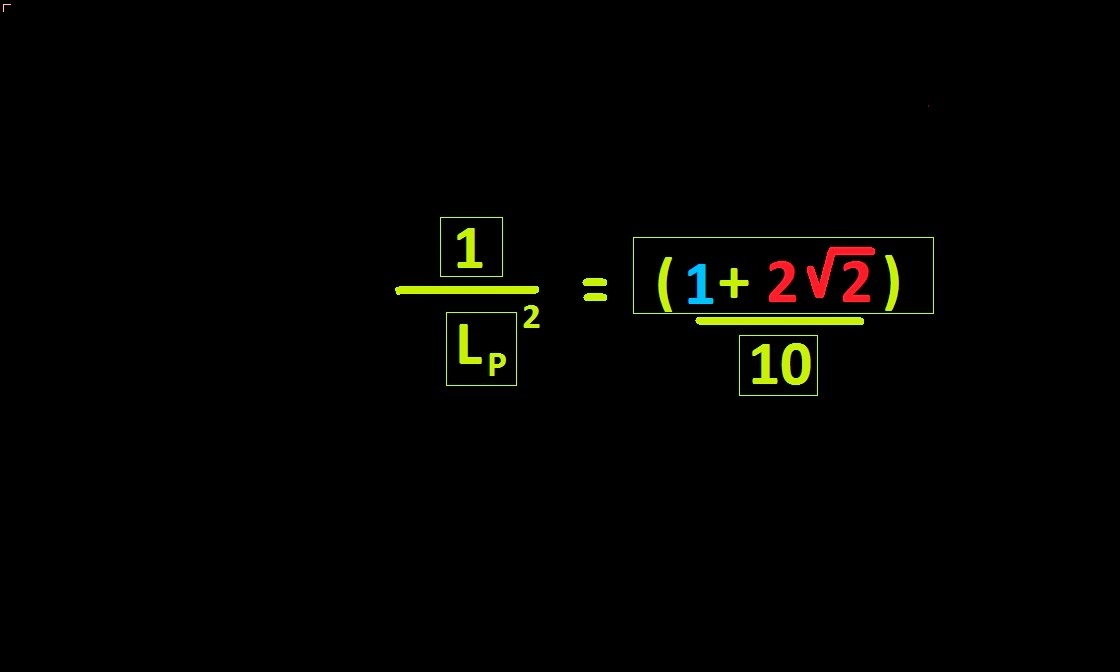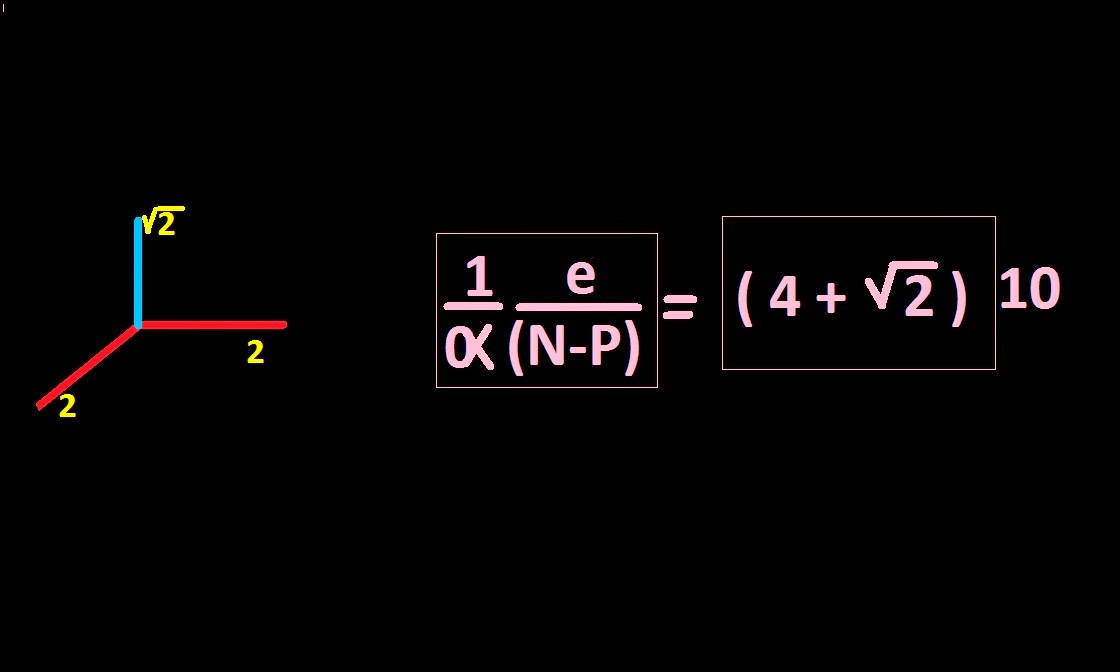through the "magnifying glass" ()()()()()()()()()()()()()()()()()()()()()()()()()()()()
through the "magnifying glass" ()()()()()()()()()()()()()()()()()()()()()()()()()()()() Past year I bought a nice device .
without trade mark we call it monday ,
because the day we bought it .
Like a special lens it's able
to watch scientific numbers
under a geometrical point of view,
applying one set of few parameters
(see images in this page)
To test monday's skills
we'll gather all type of data .
Searching in the internet's published issues
At the bottom of this page
there is a collection of
'' geometric - entertainment '' in wich
we're using , most of times , the significant figures
of some physical constants and other scientific values .
It's worth to say that the source of the values used
are
The NIST (That is CODATA recomended values ).
Monday's tool-kit .
1- Starting values : Numbers described in the following figure :
Two physical concepts inspire us :
2-
Fractal : Structure that has the same appearance at different scale . In reference to that will use the series (
32+16+2+1) or any other numerical series akin to that .
3-
Action : An atribute of a physical system product of the energy and duration of a process .Combining some of the ítems descibed before . For example take a look at an approximation to
Pi that we obtained combining the series (51) and starting values (
g + j ) :
Right triangle in wich the sum of the legs is close to Pi .
According to the formula described above will draw other ways to depict
Pi besides the typical circle :
Ways to draw Pi .
On the other hand will use two geometric algorithms clearly analogous to derivative and integral calculus :
One formula we've used several times . It includes the
parameter
d described in ''starting values'' and Pi :
MONDAY'S SHELL ALGORITHM .
For instance will illustrate with the following
equation in wich we use four constants .
Significant figures writed in brackets :
compton wavelength : [242631]
proton wavelength :[132141]
Planck constant : [662607]
electron volt : [16021765]
Planck constant , electron volt , compton wavelength , proton wavelength .
............................................................................................................................
PLANCK CONSTANT .
The significant figures of the Planck constant,
h :[662607]
As for the elementary charge ,
e :[16021765]
Planck constant in relation to electron volt .
-----------------------------------------------------------------------------------------
Planck constant - electron volt .
eV:[16021765]
h :[662607]
Elementary charge - Planck constant .
-----------------------------------------------------------------------------------------
Boltzmann constant approximation .
Significant digits of the values :
Planck constant ,
h :[662607]
Boltzmann constant ,
K : [138065]
Boltzmann constant , Planck constant .
....................................................................................................
Proportionality between Planck mass and nucleon mass .
Using the significant figures of values , ( in eV units ).
Neutron mass : [939565]
Proton mass : [938272]
Planck mass : [ 1221 ]
Planck mass - Nucleon mass .
----------------------------------------------------------------------------------------------
MONDAY'S SIGH ALGORITHM .
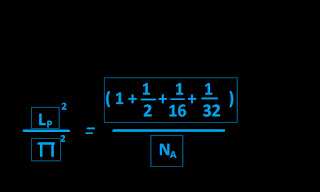
Will to explore relations among one couple of values (V1 , V2) , the series ''255'' and Avogadro's constant . The following figuration shows the basic rule .
MONDAY'S SIGH ALGORITHM .
For instance we've performed one recreational view of
Planck's length based upon
''sigh's algorithm'' :
Items used in the formula (significant figures) are :
Planck length : [161616]
Avogadro's number : [60221413]
Planck length - Avogadro's number .
--------------------------------------------------------------------------------------------
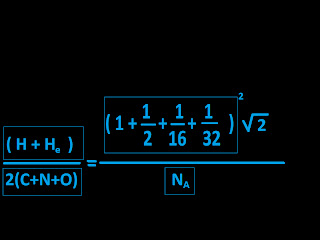
Application of sigh algorithm to the mass of some primordial elements .
Values involved in the formula :
Hydrogen :[1007825]
Helium :[40026]
Carbon :[ 12 ]
Nitrogen :[ 14 ]
Oxygen : [ 16 ]
Hydrogen , Helium , Carbon , Nitrogen , Oxygen mass .
..........................................................................................................................
Relationship between Planck mass and proton mass .
Significant values given in electronvolts :
Planck mass :[122096]
Proton mass : [938272]
Planck mass , proton mass .
.......................................................................................................................................
The case in wich Black hole entropy is equal to Boltzmann constant :
Inspirated by
Bekenstein-Hawking formula of black hole entropy , will describe
a numerical curiosity based upon series
51 and a surface equivalent to square root of two .
Lp , Planck length : [161616]
Black hole entropy , Boltzmann constant .
If we write two new items in the above formula , will obtain the inverse of fine structure constant :
Fine structure constant-Planck constant (eV)
........................................................................................................................
Neutron - proton mass ratio .
Neutron mass , in eV : [939565] . Proton mass : [938272]
Neutron-proton mass ratio .
...........................................................................................................................
Relationship among Planck mass , proton mass , Planck constant and Boltzmann constant :
Planck mass : [21765]
Proton mass : [167262]
Boltzmann constant : [138065]
Planck constant : [662607]
Avogadro's number : [602214]
Planck mass - proton mass . Boltzmann constant - Planck constant .
........................................................................................................................
Geometric curiosity about gravitation constant , speed of light , electron mass and Compton wavelength :
Significant figures of constants ,
G :[66734] C :[299792458] em :[9109382]
/\c : [242631]
Newtonian constant of gravitation , electron mass .
.....................................................................................................................
Nucleon energy in relation to Planck constant gives frequency mode of vibration .
Neutron mass + Proton mass :[334755]
Planck constant : [662607]
Avogadro number : [602214]
Speed of light : [299792458]
Nucleon frecuency mode of vibration .
..........................................................................................................................
The critical density of the universe in relation to dark energy parameter .
Here we apply the parameter
''omega-lambda'' :[0.696] as the Planck mission shows .
Also will write
critical density formula as mass-energy equivalent .
G : [66734]
HO : [ 698 ]
Universe critical density - dark energy .
............................................................................................................................
Relationship between Newtonian constant of gravitation over h bar c and nucleon mass :
G* :[6708] , N , neutron mass : [939565] , P , proton mass : [938272]
Newtonian constant of gravitation over h bar c .
...........................................................................................................................
Volume called (301) :
Volume (301)
V(301) combined with
Pi and placed in a surface (artistical depiction) :
Surface Pi(301)
.........................................................................................................................
Recreational look at the quantum vacuum force at an individual case of frequency mode of vibration .
Significant digits of values used in the following approximation :
h Planck constant :[662607]
C , speed of light in vacuum : [29979246] LP , Planck length : [161616]
Quantum vacuum force .
Now let us compare both equations posted before , that is the
Planck force and the above
vacuum force :
Vacuum force in relation to Planck force .
............................................................................................................................
Obtaining the mass of the electron and the Compton wavelength from vacuum force (and viceverse) :
em : [9109382] /\c : [242631] tp , Planck time : [539095]
Electron force (electron acceleration) .
........................................................................................................................
Planck momentum :
mp , Planck mass : [21766] C , speed of light in vacuum [299792458]
Alpha , fine structure constant : [7297353]
Planck momentum .
........................................................................................................................
Quantum energy at Planck temperature :
Here we'll apply Wien's law (peak wavelength)
h , Planck constant :[662607] C , speed of light in vacuum :[299792458]
/\m = b/Tp (Wien's law) where b = [289777] and Tp :[141676]
Quantum energy at Planck temperature .
..........................................................................................................................
Numerical curiosity among higgs boson , Planck mass , Proton mass and W boson mass .
After
Particle data group published issue , the mass of the particles described below are :
Hº , Higgs boson :[126]
P , proton mass :[938272]
W boson : [804]
mp , Planck mass :[1221]
Higgs boson , Planck mass .
............................................................................................................................
An individual case in wich Casimir force ''is equal'' to gravity force .
Howsoever our intention is merely recreational , we will refrain from using powers of ten .
h(bar) , reduced Planck constant : [1054572]
c , speed of light in vacuum : [299792458]
Casimir force - gravity force .
........................................................................................................................
Proton-proton collision in relation to (g + j ) values and the series 51 .
Below , values of the particles involved :
h/e Planck constant in eV : [41356675]
Proton colission geometry .
..........................................................................................................................
Nuclear fusion akin to above expression .
(A rare case in this blog where it is not neccesary to use
significant figures )
All units are MeV :
n , neutron mass = 939.565 He , Helium-4 binding energy = 28.3 ER , energy released = 17.59
H2 , deuterium binding energy = 2.22452 H3 , tritium b.e. = 8.482
Nuclear fusion reaction geometry .
.........................................................................................................................
Numerical curiosity in Hawking formula for black hole entropy .
( It is striking that the right side of the equation is equal to the above formula of nuclear fusión ?)
Significant figures of constants :
Lp , Planck length : [161616] KB , Boltzmann constant : [138065] C , speed of light in vacuum : [299792458] h , Planck constant : [662607] G , Newtonian constant of gravitation : [66736]
Hawking's black hole entropy .
..........................................................................................................................
Gravitational potential energy in relation to the physical Action of one photon .
G : [66735]
mp : [21765]
h : [662607]
C : [299792458]
Gravitational potential energy - photon action .
.......................................................................................................................
Gravitational potential energy between Earth - Moon
(Just for fun) what about gravitational potential energy between the Earth and the Moon , both separated by the distance light travels in one second .
Significant figures:
Mass of the Earth :[ 5972 ] Mass of the Moon : [ 7347 ]
G : [6674]
C : [299792458]
h : [662607]
Earth - Moon gravitational potential
..........................................................................................................................
............................................................................................................................
A geometric view at some coupling constants .
The following formula relates fine structure constant (
alpha- EM ), Strong coupling constant (
alpha-s) and gravitational coupling constant (
alpha''- G) that refers the ratio of the mass of the proton and the Planck mass , squared .
As for the values (according to
Particle data group ) :
alpha-em = 0.007297353
alpha-s = 0.1189
alpha''-G = 5.905 x 10^-39 .
Physical coupling constants geometry .
..............................................................................................................................
A geometric view at some cosmological parameters .
According to
Planck misión data the values of the cosmological parameters described below are :
omega-c = 0.268
omega-/\ = 0.683
omega-b = 0.049
cosmological parameters geometry .
..............................................................................................................................
A recreational look at the Planck scale.
When write Physical coupling constants and cosmological parameters in the way in wich is described below , we obtain a simple geometric value that agree with the Planck scale :
Planck scale geometry .
...............................................................................................................................
Powers of ten geometry .
Starting length and Surface .
The formula described below is inspired by the two preceding images . The left side of the equation belongs to the physical world . The right side belongs to the geometric realm .
As for the Planck length , the recommended value in S.I. units : 1.6162 x 10^-35 m .
Planck's area geometry .
...........................................................................................................................
Geometric relationship among the mass of the electron , the neutron and the proton .
Symbol
alpha refers to fine structure constant = 0.007297353
The mass expressed in electronvolts :
e = 0.51009989 MeV
N = 939.56536 MeV
P = 938.272 MeV
Electron mass,neutron mass,proton mass ,fine structure constant .
......................................................................................................................
Geometric ratio between electron mass and Planck mass .
electron mass = 0.511 x 10^6 electronvolts
Planck mass = 1.221 x 10^28 electronvolts
Avogadro's number = 6.02214 x 10^23
Electron mass - Planck mass ratio
.........................................................................................................................
Planck temperature,Planck frequency,today's temperature,today's frequency .
Wp = 1.855 x 10^43 Hz , Wt = 1.602 x 10^11 Hz
Tp = 1.417 x 10^32 K , Tt = 2.725 K
Avogadro's number = 6.022 x 10^23
Planck frequency , today's frequency , Planck temperature , today's temperature.
.........................................................................................................................
Today's energy density of the universe - Planck's energy density :
The CMB (cosmic microwave background) temperature of
2.725 K coresponds to an energy
density of
0.26 eV . On the other hand Planck's energy density is the value obtained by dividing
Planck's energy over Planck's volume =
2.892 x 10^132 eV .
As for Avogadro's number =
6.02214 x 10^23
Today's energy density - Planck energy density
.............................................................................................................................
A geometric value resulting from relationship among density-temperature-frequency in Planck's era and in the present Universe .
Densities values were previously described . Today's temperature =
2.725 K
Planck temperature =
1.417 x 10^32 K . Planck frequency =
1.855 x 10^43 Hz
Today's frequency , according to CMB (cosmic microwave background) =
1.602 x 10^11 Hz
Note the Planck scale squared .
Density , Temperature , Frequency , Geometry .
................................................................................................................................
As for the age of Universe in relation to several physical constants .
According to the data of
Planck mission the age of Universe to is close to 4.353 x 10^17 seconds
The other values described below are : speed of light , Planck's length and Avogadro's number .
Note that the
Planck scale appears explicitly in the formula .
Age of Universe , Planck length , speed of light .
..........................................................................................................................
Particular view of ideal gas law :
Starting from ideal gas law will consider a special
gas inside a particular cylinder under Planck
temperature . The following formula suggest that resulting pressure is the inverse of the gravitational
constant
G .
Ideal gas law geometry .
......................................................................................................................
Ideal gas law in a sphere .
Let's see what happens if the gas is in a sphere instead of a cylinder :
Gas law in a sphere .
.............................................................................................................................
Ideal gas law in a sphere whose radius is Planck length .
Note that in the equation appears
Avogadro number (in addition to the Avogadro number implicitly associated to the constant
R) .
Gas law in a Planck sphere .
.............................................................................................................................
Ideal gas law in the case in wich Planck force is involved .
After assigning different values to the variables of the equation , after making the relevant calculations appeared the value of the fine structure constant (
Alpha ) . By the way , Planck force multiplied by
Pi is equal to vacuum force if we consider Planck frequency .
Ideal gas law , Planck force .
.........................................................................................................................
Planck temperature - today temperature .
According to series
51 and the rectangle
( g + j ) depicted before , will describe the ratio between Planck temperature , 1.4168 x 10^32 K and today's temperature (according the Cosmic microwave background) , 2.7255 K .
Planck temperature-today temperature .
........................................................................................................................
Production of Higgs boson from electron-positron collision .
Consider the case in wich one electron collides with a positron . The two can merge to form a virtual
W boson wich can then emit a Higgs boson .
As for the masses involved (GeV) :
electron = 0.000511 ,
W = 80.4
Note that the right side of the equation belongs to the same that those related to nuclear fusión , black hole entropy and proton - proton collision , all described before .
Higgs boson from fermions .
..................................................................................................................................
Production of Higgs boson from proton-proton collision :
Follows another one example of the use of the series (51) and the symmetry (
g + j )although in this case appears only one value (square root of two). The case in wich two protons collide and a Higgs boson results after the event . The mass of proton = 0.938272 GeV
Higgs boson mass (published) = 124.99 GeV .
Higgs boson from Proton collision .
..........................................................................................................................
..........................................................................................................................
RECREATIONAL SCIENCE .
EASY EQUATIONS FOR A COMPLEX UNIVERSE.
We recently made an article concerning the geometry of the Universe . The paper named :
The Universe as a Torus .
UNIVERSE GEOMETRY EQUIVALENCE .
In that article as in other will apply the most simple geometry , looking for elementary symmetries.
Write down in this blog successive contributions on these issues .
In addition to numerical equivalence between two volumes ( torus-Avogadro) and (polyhedron-speed of light) there is a third equivalence : ( proton Compton wavelength cubed -Torus volume) .
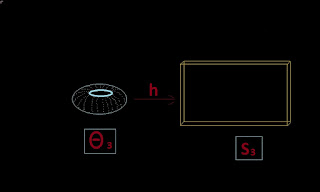
Definition of Torus-3 :
Definition of C3 :
Numerical equivalence Torus-3 and C3 :
(Inverse) Numerical relationship Avogadro's number - Proton Compton wavelength :
(Inverse)Numerical equivalence . Torus 3 and Proton Compton wavelength cubed :
An other universe geometry equivalence depiction :
Geometric relationship between cosmological constant and Avogadro number :
Surface area equivalences . An alternative view of the above formula :
An 'elementary' Surface used as numerical
distiller :
Geometric
distilled from proton energy :
The Torus , the Hubble parameter and a numerical frame .Where
h is a dimensionless number Assumed
h = 0.7:
Alternative view when two volume are retated :
Schematic depiction of the above equation :
An other
vectorial look in wich values involved include : Euler number and inverse of fine structure constant . Besides the Torus-3 :
Development of the Torus-3 from symmetry (
g + j ) , the Neutron-Proton mass ratio N/P and the series akin to the series (32+16+2+1) used time ago for an numerical approximation to Pi . Symbol e refers to Euler number :
The evolution of a (particular) Universe .
Numerical equivalence between (
A B^2 ) and an other type of Torus :
According to above equations will depict the development from (smooth) universe , Torus-03 to a granulated one , ie Torus - 3 in wich Avogadro's number appears .
geometric beginning and evolution of a Universe
.................................................................................
Torus-3 , Planck mass-energy and the mass-energy of the electron from the geometrical point of view .
........................................................................................................
Hubble parameter , Proton Compton wavelength , Parsec , Speed of light .
Relationship between Planck energy density and (today) Dark energy density :

 Biology and geometry por A . Coe se encuentra bajo una Licencia Creative Commons Atribución-NoComercial 3.0 Unported.
Biology and geometry por A . Coe se encuentra bajo una Licencia Creative Commons Atribución-NoComercial 3.0 Unported.





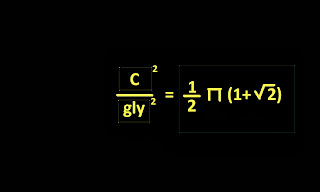









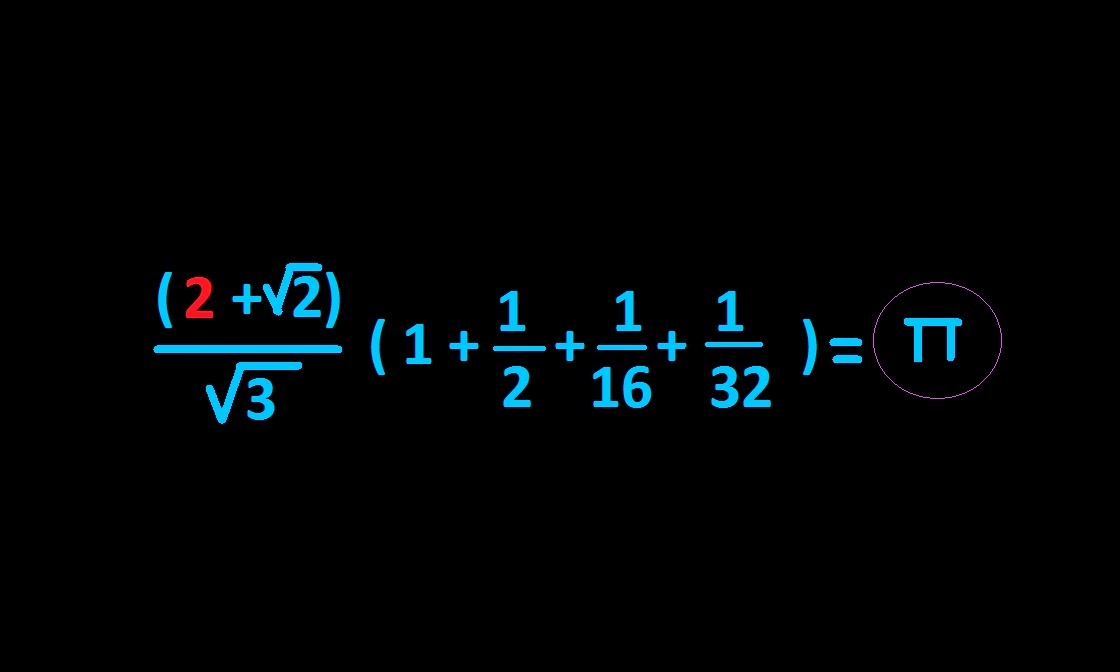


.bmp)




.bmp)